T-rule

T-rules, or transformation rules, are rules that alter the state of nodes. They are used for normalization, for syntactic analysis and for semantic interpretation. The set of the t-rules forms the Transformation grammar, or T-Grammar.

Basic Symbols

Basic symbols used in the UNL framework

Symbol	Definition	Example
( )	node	(%a)
" "	string	"went"
[ ]	natural language entry (headword)	[go]
[[ ]]	UW	[[to go(icl>to move)]]
//	regular expression	/a{2,3}/ = aa,aaa
rel(x;y)	relation	agt(kill;Peter)
^	not	^a = not a
{ | }	or	{a|b} = a or b
%	index for nodes, attributes and values	%x
:	scope ID	:01
#	index for sub-NLWs	#01
=	attribute-value assignment	POS=NOU
!	rule trigger	!PLR
&	merge operator	%x&%y
?	dictionary lookup operator	?[a]

Basic Concepts

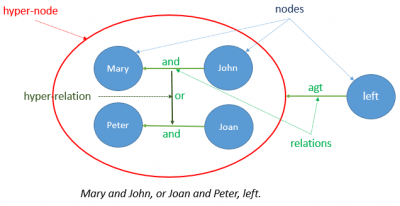
Node

A node is the most elementary unit in the graph. It is the result of the tokenization process, and corresponds to the notion of "lexical item". At the surface level, a natural language sentence is considered a list of nodes, and a UNL graph a set of relations between nodes.

Relation

In order to form a natural language sentence or a UNL graph, nodes are inter-related by relations. In the UNL framework, there are three different types of relations: the linear (list) relation, syntactic relations and semantic relations.

Hyper-Node

A hyper-node is a sub-graph, i.e., a scope: a node containing relations between nodes.

Hyper-Relation

A hyper-relation is a relation between relations.

Syntax

The Transformation Rules follow the very general formalism

α:=β;

where the left side α is a condition statement, and the right side β is an action to be performed over α.

Types of Transformation Rules

Natural language sentences and UNL graphs are supposed to convey the same amount of information in different structures: whereas the former arranges data as an ordered list of words, the latter organizes it as a hypergraph. In that sense, translating from natural language into UNL and from UNL into natural language is ultimately a matter of transforming lists into networks and vice-versa.

The UNDLF generation and analysis tools assume that such transformation should be carried out progressively, i.e., through a transitional data structure: the tree, which could be used as an interface between lists and networks. Accordingly, the UNL Grammar states seven different types of rules (LL, TT, NN, LT, TL, TN, NT), as indicated below:

• ANALYSIS (NL-UNL)
  • LL - List Processing (list-to-list)
  • LT - Surface-Structure Formation (list-to-tree)
  • TT - Syntactic Processing (tree-to-tree)
  • TN - Deep-Structure Formation (tree-to-network)
  • NN - Semantic Processing (network-to-network)

• GENERATION (UNL-NL)
  • NN - Semantic Processing (network-to-network)
  • NT - Deep-Structure Formation (network-to-tree)
  • TT - Syntactic Processing (tree-to-tree)
  • TL - Surface-Structure Formation (tree-to-list)
  • LL - List Processing (list-to-list)

The NL original sentence is supposed to be preprocessed, by the LL rules, in order to become an ordered list. Next, the resulting list structure is parsed with the LT rules, so as to unveil its surface syntactic structure, which is already a tree. The tree structure is further processed by the TT rules in order to expose its inner organization, the deep syntactic structure, which is supposed to be more suitable to the semantic interpretation. Then, this deep syntactic structure is projected into a semantic network by the TN rules. The resultant semantic network is then post-edited by the NN rules in order to comply with UNL standards and generate the UNL Graph.

The reverse process is carried out during natural language generation. The UNL graph is preprocessed by the NN rules in order to become a more easily tractable semantic network. The resulting network structure is converted, by the NT rules, into a syntactic structure, which is still distant from the surface structure, as it is directly derived from the semantic arrangement. This deep syntactic structure is subsequently transformed into a surface syntactic structure by the TT rules. The surface syntactic structure undergoes many other changes according to the TL rules, which generate a NL-like list structure. This list structure is finally realized as a natural language sentence by the LL rules.

As sentences are complex structures that may contain nested or embedded phrases, both the analysis and the generation processes may be interleaved rather than pipelined. This means that the natural flow described above is only "normal" and not "necessary". During natural language generation, a LL rule may apply prior to a TT rule, or a NN rule may be applied after a TL rule. Rules are recursive and must be applied in the order defined in the grammar as long as their conditions are true, regardless of the state.

List-to-List Rules

The list-to-list (LL) rules are used for processing lists, both in analysis and in generation. In analysis, these rules are used for pre-editing the natural language sentence and preparing the input to the syntactic module; in generation, they are used for post-editing the output of the syntactic module and generating the natural language sentence.

There are 5 different subtypes of LL rules:

LL rules

ACTION	RULE	DESCRIPTION
ADD	(%x):=(%x)(%y);	The node %y is added to the right of the node %x
	(%x):=(%y)(%x);	The node %y is added to the left of the node %x
DELETE	(%x):=-(%x);	The node %x is deleted.
	(%x):=;
REPLACE	(%x):=(%y);	All the instances of the node %x will be replaced by the node %y
MERGE	(%x)(%y):=(%x&%y);	The nodes %x and %y will be merged

Where %x and %y are nodes.

Tree-to-Tree Rules

The tree-to-tree rules (TT) are used for processing trees, both in analysis and in generation. During analysis, these rules are used for revealing the deep structure out of the surface structure; in generation, they are used for transforming the deep into the surface syntactic structure.

Syntactic relations are n-ary: they can have as many arguments (nodes) as necessary.

There are 3 different subtypes of TT rules:

TT rules

ACTION	RULE	DESCRIPTION
ADD RELATION	SYN1(%x;%y):=+SYN2(%w;%z);	The relation SYN2 between the nodes %w and %z will be added to the graph containing the relation SYN1 between the nodes %x and %y
DELETE RELATION	SYN(%x;%y):=-SYN(%x;%y);	The relation SYN between the nodes %x and %y will be deleted (the nodes %x and %y will not be deleted)
	SYN(%x;%y)=;
REPLACE RELATION	SYN1(%x;%y):=SYN2(%w;%z);	The relation SYN1 between the nodes %x and %y will be replaced by the relation SYN2 between the nodes %w and %z

Where SYN is a syntactic relation, and %x, %y, %z and %w are nodes.

As syntactic relations are n-ary, the REPLACE RELATION may also be used to ADD or DELETE nodes.

Special types of TT replace relations

ACTION	RULE	DESCRIPTION
ADD NODE	SYN(%x;%y):=SYN(%x;%y;%z);	The binary relation SYN between the nodes %x and %y is replaced by a ternary relation SYN between the nodes %x, %y and %z
DELETE NODE	SYN(%x;%y):=SYN(%y);	The binary relation SYN between the nodes %x and %y is replaced by a unary relation SYN with the node %y

Where SYN is a syntactic relation, and %x, %y and %z are nodes.

Network-to-Network Rules

The network-to-network rules (NN) are used for processing networks, both in analysis and in generation. During analysis, these rules are used for post-editing the semantic network structure derived from the syntactic module in order to generate the UNL graph; in generation, they are used for pre-editing the UNL graph, transforming it into a semantic network that would be more appropriate for sentence generation.

There are 3 different subtypes of NN rules:

NN rules

ACTION	RULE	DESCRIPTION
ADD RELATION	SEM1(%x;%y):=+SEM2(%w;%z);	The relation SEM2 between the nodes %w and %z will be added to the graph containing the relation SEM1 between the nodes %x and %y
DELETE RELATION	SEM(%x;%y):=-SEM(%x;%y);	The relation SEM between the nodes %x and %y will be deleted (the nodes %x and %y will not be deleted)
	SEM(%x;%y)=;
REPLACE RELATION	SEM1(%x;%y):=SEM2(%w;%z);	The relation SEM1 between the nodes %x and %y will be replaced by the relation SEM2 between the nodes %w and %z

Where SEM is any of the existing UNL relations, and %x, %y, %z and %w are nodes.

List-to-Tree Rules

The list-to-tree (LT) rules are used to parse the list structure into a tree structure.
There are 2 different subtypes of LT rules:

LT rule

ACTION	RULE	DESCRIPTION
ADD	(%x)(%y):=+SYN(%x;%y);	The relation SYN is created between the nodes %x and %y if there is a linear relation between them (the linear relation is not deleted)
REPLACE	(%x)(%y):=SYN(%x;%y);	The linear relation between %x and %y is replaced by the relation SYN between the same nodes (i.e., the linear relation is deleted)

Where SYN is a syntactic relation, and %x and %y are nodes.

Tree-to-List Rules

The tree-to-list (TL) rules are used to linearize the tree structure into a list structure. There is one single type of TL rule:

There is a single type of TL rule:

TL rule

ACTION	RULE	DESCRIPTION
REPLACE	SYN(%x;%y):=(%x)(%y);	The relation SYN between %x and %y is replaced by a linear relation between %x and %y

Where SYN is a syntactic relation and %x and %y are nodes.

Tree-to-Network Rules

The tree-to-network (TN) rules derive a semantic network out of a syntactic tree.

There are 2 types of TN rules:

TN rule

ACTION	RULE	DESCRIPTION
ADD	SYN(%x;%y):=+SEM(%w;%x);	The semantic relation SEM between the nodes %w and %x is created if there is a syntactic relation SYN between the nodes %x and %y
REPLACE	SYN(%x;%y):=SEM(%x;%y);	The syntactic relation SYN between the nodes %x and %y is replaced by the semantic relation SEM between the same nodes.

Where SYN is a syntactic relation, SEM is a semantic relation, and %x, %y, %w and %z are nodes.

Network-to-Tree Rules

The network-to-tree (NT) rules reorganizes the network structure as a deep tree structure.

There are two types of TN rules:

NT rule

ACTION	RULE	DESCRIPTION
ADD	SEM(%x;%y):=+SYN(%w;%x);	The syntactic relation SYN between the nodes %w and %x is created if there is a semantic relation SEM between the nodes %x and %y
REPLACE	SEM(%x;%y):=SYN(%x;%y);	The semantic relation SEM between the nodes %x and %y is replaced by the syntactic relation SYN between the same nodes.

Where SYN is a syntactic relation, SEM is a semantic relation, and %x, %y, %w and %z are nodes.

Special types of transformation rules

• A-rule is a specific type of T-rule used for affixation (prefixation, infixation, suffixation)
• C-rule is a specific type of T-rule used for composition (word formation in case of compounds and multiword expressions)
• L-rule is a specific type of T-rule used for handling word order
• N-rule is a specific type of T-rule used for segmenting sentences and normalizing the input text
• S-rule is a specific type of T-rule used for handling syntactic structures

General properties of transformation rules

PRIORITY

Rules are applied serially, according to the order defined in the grammar. The first rule will be the first to be applied, the second will be the second, and so on. In case of the same rule being applicable more than once, rules are applied from left to right (in case of lists) and top-down (in case of graphs).

For instance:

List structure

INPUT = [a][ ][beautiful][ ][book]

GRAMMAR =

RULE#1: ([ ]):=; (delete the blank space)

RULE#2: ([beautiful])([ ])([book]):=([book])([beautiful]); (replace "beautiful+blank+book" by "book+beautiful")

RESULT:

INITIAL STATE: [a][ ][beautiful][ ][book]

STATE#1: [a][beautiful][ ][book] (the RULE#1 is the first applicable rule to appear in the grammar and, therefore, is the first one to be applied, and it will apply to the leftmost blank)

STATE#2: [a][beautiful][book] (the RULE#1 applies a second time, because there is a second blank space in the input)

FINAL STATE: [a][beautiful][book] (the RULE#2 never applies, because its condition is no longer true after the second application of RULE#1)

Graph structure

INPUT = mod(book,beautiful)mod(book,new)

GRAMMAR =

RULE#1: mod(%x;%y):=NA(%x;%y); (replace the mod relation between the nodes %x and %y by a NA relation between the same nodes)

RESULT:

INITIAL STATE: mod(book,beautiful)mod(book,new)

STATE#1: NA(book,beautiful)mod(book,new) (the RULE#1 is the first applicable rule to appear in the grammar and, therefore, is the first one to be applied, and it will apply to the topmost relation, i.e., the first one to appear in the graph)

STATE#2: NA(book,beautiful)NA(book,new) (the RULE#1 applies a second time, because there is a second mod relation to be replaced)

FINAL STATE: NA(book,beautiful)NA(book,new)

RECURSIVENESS

Rules are applied recursively as long as their conditions are true. Because of that, special attention should be paid to ADD rules:

• (%x,A):=(%x,+B); (creates an infinite loop, because the feature B will be added infinitely to the node %x)
  

In order to avoid the endless repetition, the condition side must be changed to (%x,A,^B):=(%x,+B); (the rule applies only once)

• REL1(%x;%y):=+REL2(%x;%z); (creates an infinite loop, because the REL2 will be added infinitely to the graph)
  

In order to avoid the endless repetition, the condition side must be changed to REL1(%x;%y)^REL(%x;%z):=+REL2(%x;%z); OR REL1(%x,^BREAK;%y):=+REL2(%x,+BREAK;%z); (the rule applies only once)

COMPREHENSIVENESS

Grammars are applied comprehensively as long as there is at least one applicable rule.

CONSERVATION

Rules affect only the information clearly specified. No relation, node or feature is deleted unless explicitly informed.

For instance, in the examples below, the source node of the “agt” relation preserves, in all cases, the value “a”. The only change concerns the feature “c”, which is added to the source node of the “agt” in the first two cases; and the feature “b”, which is deleted from the target node in the third case.

agt(a;b):=agt(c;);

agt(a;b):=agt(+c;);

agt(a;b):=agt(;-b);

In any case, the ADD and DELETE rules (i.e., when the right side starts with “+” or “-“) preserve the items in the left side, except for the explicitly deleted ones:

INPUT: agt(%x;%y) obj(%x;%z) tim(%x;%w)

RULE: agt(%x;%y) ^mod(%x;%k):=+mod(%x;%k);

OUTPUT: agt(%x;%y) obj(%x;%z) tim(%x;%w) mod(%x;%k)

or

INPUT: agt(%x;%y) obj(%x;%z) tim(%x;%w)

RULE: agt(%x;%y):=-agt(%x;%y);

OUTPUT: obj(%x;%z) tim(%x;%w)

SCOPE

LL and LT rules apply over nodes, whereas NN, TT, NT, TN and TL rules apply over relations.

Nodes may be deleted only through LL and LT rules (i.e., when appearing in the left side of rules).

(A):=; (the node containing the feature "A" is deleted)

(%A,A):=-(%A); (the node containing the feature "A" is deleted - the same as above)

(%A,A)(%B,B):=(%A); (the node containing the feature "B" is deleted because not present in the right side - see indexes)

(%A,A)(%B,B)(%C,C):=REL(%A;%B); (the node containing the feature "C" is deleted, because not present in the right side - see indexes)

Nodes may not be deleted through NN, TT, NT, TN and TL rules (i.e., when not appearing in the left side of rules).

REL(%A,A;%B,B;%C,C):=(%A)(%B); (the relation between the nodes containing the features "A", "B" and "C" is replaced by a linear relation between the nodes containing the features "A" and "B". The node "C", however, is not deleted, even though absent from the right side - see indexes)

Relations may be deleted directly through NN, TT, NT, TN and TL rules, and indirectly through LL and LT rules (when their nodes are deleted).

REL(A;B):=; (The relation between the nodes containing the features "A" and "B" is deleted, but the nodes are preserved)

REL(A;B)REL(%C,C;%D,D):=REL(%C;%D); (The relation between the nodes containing the features "A" and "B" is deleted; its nodes and the relation between the nodes containing the features "C" and "D" are preserved)

(A):=; (The node containing the feature "A" is deleted, as well as all relations in which it figures as an argument)

INDEXATION

All instances of the same node must be co-indexed (or they will be considered different nodes). See Indexation.

(%a)(%b):=(%a); (delete the node %b)

(%a)(%b):=(%b); (delete the node %a)

rel(%a;%b):=rel(%a;%c); (replace the node %b by the node %c; the node %a does not undergo any change)

SYN(%x,^NUM;%y,NUM):=SYN(%x,NUM=%y;%y); (copy the value of the attribute NUM from the node %y to the node %x)

ACTION

Rules may add or delete values to the source and the target nodes, but only in the right side items:

agt(a;b):=agt(+c;);

agt(a;b):=agt(;-b);

CONJUNCTION

Both the left and the right side of the rule may have as many items as necessary, as exemplified below:

SEM(A;B)SEM(C;D)SEM(E;F):=SEM(G;H)SEM(I;J)SEM(K;L);

DISJUNCTION

The left side of the rules may bring disjuncts, but not the right side. Disjuncts must be represented between {braces} and must be separated by |.

{SEM(A;B)|SEM(C;D)}^SEM(E;F):=+SEM(E;F);

SEM(A;B){SEM(C;D)|SEM(E;F)}:=-SEM(A;B);

agt(VER,{V01|V02};NOU,^SNG}:=;

REGULAR EXPRESSIONS

The left side of the rules may bring regular expressions between "/":

/(agt|obj|aoj)/(A,%a;B,%b):=VS(%a;%b);

The rule above applies in case of agt(A;B), obj(A;B) and aoj(A;B)

/[a-z]{2,3}/(A,%a;B,%b):=VS(%a;%b);

The rule above applies in case of any sequence of two or three alphabetic characters in the position of relation of A and B

agt(/(VER|NOU)/,%a;%b):=VS(%a;%b);

The rule above applies in case of VER and NOU as features of the first node of the relation "agt"

agt(POS=/(VER|NOU)/,%a;%b):=VS(%a;%b);

The rule above applies in case of VER and NOU as values of the attribute POS of the first node of the relation "agt"

CONCISION

In order for rules to be as small as possible, the source and the target nodes may be simple place-holders or indexes:

cob(;):=obj(;);

tim(%01;[[in]]),obj([[in]];%02):=tim(%01;%02);

tim(VER,%01;[[in]]),obj([[in]];NOU,%02):=tim(%01;%02);

tim(VER;in),obj(in;NOU):=tim(;%04);

In the DELETE rules, the right side may be omitted in case of deletion of the entire left side:

obj(PRE;):=;

READABILITY

There can be blank spaces between variables and symbols. Comments can be added after the “;”.

obj ( ; ) := ; this rule deletes every “obj” relation.

COMMUTATIVITY

Inside the same side of NN, NT, TT and TN rules, the order of the factors does not affect the result

SEM(A;B):=SEM(C;D)SEM(E;F); IS EQUIVALENT TO SEM(A;B):= SEM(E;F)SEM(C;D);

SYN(A;B):=SYN(C;D)SYN(E;F); IS EQUIVALENT TO SYN(A;B):= SYN(E;F)SYN(C;D);

The order of the factors affect the result in case list-processing rules (LL, LT and TL):

(A):=(B)(C); IS DIFFERENT FROM (A):=(C)(B);

SYN(A;B):=(C)(D); IS DIFFERENT FROM SYN(A;B):=(D)(C);

(C)(D):=SYN(A;B); IS DIFFERENT FROM (D)(C):=SYN(A;B);

Additionally, the order of the features inside a relation does not affect the end result, but the order of the nodes is non-commutative.

SEM( VER,TRA ; NOU,MCL ) IS THE SAME AS SEM( TRA,VER ; MCL,NOU )

But:

SEM( VER,TRA ; NOU,MCL) IS DIFFERENT FROM SEM( NOU,MCL ; VER,TRA )

DICTIONARY RULES (see also Inflection rules inside dictionary entries)

Dictionary rules are triggered by "!"<ATTRIBUTE>:

Dictionary

[foot] "foot" (NOU, NUM(PLR:=”oo”:”ee”)) <eng,0,0>;

[city] "city" (NOU, NUM(PLR:=”y”>”ies”)) <eng,0,0>;

Grammar

(@pl, NUM):=(!NUM,-@pl);

Output

foot>feet

city>cities

Formal Syntax of Transformation Rules

<TRANSFORMATION RULE> ::= <NN RULE> | <NT RULE> | <TT RULE> | <TL RULE> | <LL RULE> | <LT RULE> | <TN RULE>
<NN RULE>             ::= (<SEM>)+ ":=" ( ("-"|"+")? <SEM> )* ";"
<TT RULE>             ::= (<SYN>)+ ":=" ( ("-"|"+")? <SYN> )* ";"
<LL RULE>             ::= ( "(" <NODE> ")" )+ ":=" ( ("-"|"+")? "(" <NODE> ")" )* ";"
<NT RULE>             ::= (<SEM>)+ ":=" ( <SYN> )+ ";"
<TN RULE>             ::= (<SYN>)+ ":=" ( <SEM> )+ ";"
<TL RULE>             ::= (<SYN>)+ ":=" ( "(" <NODE> ")" )+ ";"
<LT RULE>             ::= ( "(" <NODE> ")" )+ ":=" ( <SYN> )+ ";"
<SEM>                 ::= <TEXT> "(" <NODE> ";" <NODE> ")"
<SYN>                 ::= <TEXT> "(" <NODE> ";" <NODE> ")"
<NODE>                ::= ( (<DESCRIPTION>)( "," <DESCRIPTION> )* )?
<DESCRIPTION>         ::= <STRING> | <ENTRY> | <SUB-ENTRY> | <FEATURE> | <INDEX> | <RELATION>
<STRING>              ::= """<text>"""
<ENTRY>               ::= "["<entry>"]"
<SUB-ENTRY>           ::= <INDEX>"#"[01-99]
<FEATURE>             ::= <VALUE> | <ATTRIBUTE> | <ATTRIBUTE>"="<VALUE>
<INDEX>               ::= ( "%"([01-99]|[a-zA-Z_]+) )+
<RELATION>            ::= <SEM>|<SYN>
<VALUE>               ::= <TEXT>
<ATTRIBUTE>           ::= <TEXT>
<TEXT>                ::= any sequence of characters except whitespace | <REGULAR EXPRESSION>
<REGULAR EXPRESSION>  ::= "/"<PERL COMPATIBLE REGULAR EXPRESSIONS>"/"

Where:
"" = constant
+ = to be repeated one or more times
* = to be repeated zero or more times
? = to be repeated zero or one time
| = or
[x-y] = from x to y

Examples of Rules

In the examples below:

• L(A;B) is a linear (list) relation between A and B (i.e., L(A;B) = (A)(B))
  
• REL(A;B) is a non-linear (tree or network) relation between A and B
  
• %X is the index for a node
  
• :X indicates that the following relation or node is inside the hyper-node X
  
• A,B,C,D,B1,B2,B3 and B4 are features of the nodes %A,%B,%C,%D,%B1,%B2,%B3 and %B4, respectively.
  

LL RULES

INITIAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4)

LL#1: (B):=;

(Delete all nodes having the feature B, wherever they are)

FINAL STATE: L(%A;%C) L(%C;%D)

The whole hyper-node %B will be deleted, including all its nodes, no matter in which level.

LL#2: (B1):=;

(Delete all nodes having the feature B1, wherever they are)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B2;%B3) :B(%B4)

Only the node (%B1) is deleted. The relation REL is also deleted, but the node %B4 is preserved as an isolated node inside the hyper-node %B.

LL#3: ((B1)):=;

(Delete any hyper-node that contains the node having the feature B1, wherever they are);

FINAL STATE: L(%A;%C) L(%C;%D)

The whole hyper-node %B will be deleted, including all its nodes, no matter in which level.

LL#4: (B1):=(NEW);

(Add the feature “NEW” to all nodes having the feature B1)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4) (NO CHANGE IN THE NODE STRUCTURE)

There is no indexes in the left and the right side, which have the same number of nodes. This means that they are automatically co-indexed. No node is deleted or replaced. The feature “NEW” is added to the the node %B1, because it contains the feature B1. This rule provokes a look, because the feature NEW will be added indefinitely to the node %B1. In order to avoid this, the condition should be set (B1,^NEW):=(NEW);

LL#5: (%x,B1):=(%y,NEW);

(Replace any node having the feature B1 by a new node having the feature NEW)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%NEW;%B2) L:B(%B2;%B3) REL:B(%NEW;%B4)

The node %B1 is deleted and replaced by a new node %NEW. Notice that all instances of the node are replaced.

LL#6: ({(B1)|(B3)}):=;

(Delete any hyper-node that contains nodes having the features B1 or B3);

FINAL STATE: L(%A;%C) L(%C;%D)

The whole hyper-node %B will be deleted, including all its nodes, no matter in which level.

LL#7: ((B1)(B2)):=;

(Delete any hyper-node that contains the relation L(B1;B2));

FINAL STATE: L(%A;%C) L(%C;%D)

The whole hyper-node %B will be deleted, including all its nodes, no matter in which level.

LL#8: ((B1)(B3)):=;

(Delete any hyper-node that contains the relation L(B1;B3))

Nothing happens. The condition is not true in the case of the initial state indicated above.

LL#9: ((B1)):=(-feature);

(Remove the feature “feature” from any hyper-node containing a node with the feature B1)

As the left and the right side do not have indexes, they are automatically co-indexed. The co-indexation, however, is valid only to the hyper-node level, because the right side does not contain any inner node. In that sense, the feature “feature” is not removed from the inner node, but from the hyper-node.

LL#10: ((B1)):=((-feature));

(Remove the feature “feature” from anynode having the feature B1 which is inside a hyper-node)

The automatic indexation affects both levels: the hyper-node and the node, because they are equivalent. The rule is the same as (%x,(%y,B1)):=(%x,(%y,-feature));. The feature “feature” is now removed from the inner node and not from the hyper-node.

LL#11: ((%x,B1)):=((%y,NEW));

(Replace any node containing the feature B1 inside a hyper-node by a new node containing the feature 'NEW')

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%NEW;%B2) L:B(%B2;%B3) REL:B(%NEW;%B4)

The same as (%x,B1):=(%y,NEW); but inside a hyper-node (i.e., the rule applies only to the nodes having the feature B1 which are inside some other node).

LL#12: ((B1)):=((E)(F));

(Replace any node containing the feature B1 by a linear relation between two new nodes containing the features E and F, respectively)

FINAL STATE: : L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B2;%B3) REL:B(%HB;%B4) L:HB(%E;%F)

The same as (%x,B1):=(%y,E)(%z,F); but inside a hyper-node (i.e., the rule applies only to the nodes having the feature B1 which are inside some other node). The linear relation between the nodes (%B1) and (%B2) disappear, because (%B1) is an argument of a non-linear relation REL(%B1;%B4) and should be replaced, therefore, by a hyper-node instead of a simple sequence of nodes (%E)(%F), since REL((%E)(%F);(%B4)) is not possible. As a consequence, the nodes (%E) and (%F) are created inside the hyper-node %HB and may not hold any linear relation with %B2, because they are now in different scopes.

LL#13: ((B1)):=(((E)(F),-B1));

(Replace any node containing the feature B1 by a new node containing a linear relation between two new nodes containing the features E and F, respectively)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%HB;%B2) L:B(%B2;%B3) REL:B(%HB;%B4) L:HB(%E;%F)

The same as (%x,(%a,B1)):=(%x,(%b,E)(%c,F)); but inside a hyper-node (i.e., the rule applies only to the nodes having the feature B1 which are inside some other node). Differently from the previous example, the node containg the feature B1 is replaced by a hyper-node and not by two other nodes of the same level. As the system is conservative, the feature B1 has to deleted in order to prevent the rule from applying eternally.

LL#14:((B1)):=((E),(F));

(Replace the node containing the feature B1 by two new nodes containing the features E and F, respectively)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%HB;%B2) L:B(%B2;%B3) REL:B(%HB;%B4) :HB(%E) :HB(%F)

The nodes (E) and (F) no longer constitute a linear relation, and are added as isolated notes to the hyper-node. Because of that, (B1) has to be replaced, necessarily, by a hyper-node. This means that this rule will have exactly the same effect of the rule below.

LL#15:((B1)):=(((E),(F),-B1));

(Replace the node containing the feature B1 by two new nodes containing the features E and F, respectively)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%HB;%B2) L:B(%B2;%B3) REL:B(%HB;%B4) :HB(%E) :HB(%F)

The nodes (E) and (F) no longer constitute a linear relation, and are added as isolated notes to the hyper-node. As the system is conservative, the feature B1 has to deleted in order to prevent the rule from applying eternally.

LL#16: (REL(%B1;%B4)):=(NEWREL(%B1;%B5));

(Replace the relation REL between the nodes %B1 and %B4 by a new relation NEWREL between the existing node %B1 and a new node %B5)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) NEWREL:B(%B1;%B5) :B(%B4)

Nodes on both sides are automatically co-indexed, because their number is the same. Therefore, the relation on the left side is replaced by the relation on the right side in the same hyper-node. No node is deleted: notice that %B4 is still there. This is the same as REL(A;B):=REL(C;D);.

LL#17:(B1)(B2):=;

(The same as L(%B1;%B2):=; i.e., delete the linear relation between %B1 and %B2)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) :B(%B3) REL:B(%B1;%B4)

The linear relation between (%B1) and (%B2) is deleted, but the nodes (%B1) and (%B2) are preserved if part of other non-linear relations.

LL#18:(B1)(B2):=(B5);

(The same as L(%B1;%B2):=(%B5); i.e., replace the linear relation between %B1 and %B2 by %B5)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B5;%B3) REL:B(%B1;%B4)

The linear relation between (%B1) and (%B2) is replaced by %B5, but the nodes (%B1) and (%B2) are preserved if part of other non-linear relations.

LL#19:(%B1,B1)(B2):=(%B1);

(The same as L(%B1;%B2):=(%B1); i.e., replace the linear relation between %B1 and %B2 by %B1)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B3) REL:B(%B1;%B4)

The linear relation between (%B1) and (%B2) is replaced by %B1, but the nodes (%B1) and (%B2) are preserved if part of other non-linear relations.

LL#20:(B1)(%B2,B2):=(%B2);

(The same as L(%B1;%B2):=(%B2); i.e., replace the linear relation between %B1 and %B2 by %B2)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B2;%B3) REL:B(%B1;%B4)

The linear relation between (%B1) and (%B2) is replaced by %B2, but the nodes (%B1) and (%B2) are preserved if part of other non-linear relations.

LL#21:(%B1,B1)(%B2,B2):=(%B1,(%B2));

(replace the linear relation between %B1 and %B2 by the node %B1 with %B2 inside as an isolated node)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B3) REL:B(%B1;%B4) :B1(%B2)

The linear relation between (%B1) and (%B2) is replaced by %B1, but the nodes (%B1) and (%B2) are preserved if part of other non-linear relations.

LL#22: (%D,D):=(%D,-D,+D1)(%D,-D,+D2);

(Duplicate the node having the feature D, wherever they are)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D1) L(%D1;%D2) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4)

The whole hyper-node %D will be duplicated, including all its nodes, no matter in which level. Node duplication occurs only in LL rules. As the system is conservative, the feature D has to deleted in order to prevent the rule from applying eternally.

LT RULES

INITIAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4)

LT#1: (%B1,B1)(%B2,B2):=REL(%B1;%B2);

(Replace the relation L(%B1;%B2) by the relation REL(%B1;%B2))

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) REL:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4)

No node is deleted, but there’s no longer a linear relation between %B1 and %B2. There’s still, however, a linear relation between %B2 and %B3 inside the hyper-node %B.

LT#2: (%B1,B1)(%B2,B2):=+REL(%B1;%B2);

(Add the relation REL(%B1;%B2) to the graph )

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4) REL(%B1;%B2)

No node or relation is deleted. A new relation is created in the graph.

LT#3: (%B1,B1)(%B2,B2)(%B3,B3):=REL(%B1;%B2);

(Replace the relations L(%B1;%B2)L(%B2;%B3) by the relation REL(%B1;%B2))

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) REL:B(%B1;%B2) REL:B(%B1;%B4)

The node (%B3) is deleted because it is not present in the right side.

LT#4: (%B1,B1)(%B3,B3)(%B2,B2):=REL(%B1;%B2);

(Replace the relations L(%B1;%B3)L(%B3;%B2) by the relation REL(%B1;%B2))

Nothing happens. The condition is not true in this case.

LT#5: (%B1,B1):=REL(%B1;%B5); (Replace the node having the feature B1 by the relation REL(%B1;%B5))

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B2;%B3) REL:B(%HB;%B4) REL:HB(%B1;%B5)

There is no longer a linear relation between %B1 and %B2, because the node was replaced by a relation and, therefore, removed from the list structure.

LT#6: (%B1,B1):=+REL(%B1;%B5); (Add the relation REL(%B1;%B5) to the graph)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4) REL(%B1;%B5)

No node is replaced or deleted. A new relation is added to the graph.

LT#7: (REL(%B1,B1;%B4,B4)):=NEWREL(%B1;%B4); (Replace the hyper-node containing the relation REL by the relation NEWREL(%B1;%B5)

FINAL STATE: L(%A;%C) L(%C;%D) NEWREL(%B1;%B4)

The whole hyper-node %B will be replaced by the new relation. All its inner nodes not referred to in the right side will be deleted as well.

LT#8: (REL(%B1,B1;%B4,B4)):=+NEWREL(%B1;%B4); (Add the relation NEWREL(%B1;%B4) to the graph)</nowiki>

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4) NEWREL(%B1;%B4)

The hyper-node remains the same. The relation NEWREL(%B1;%B4) is added to its outer scope.

TL Rules

INITIAL STATE: L(%A;%B) L(%B;%C) REL:B(%B1;%B2) REL:B(%B1;%B3)

TL#1: REL(%B1;%B2)REL(%B1;%B3):=(%B1)(%B2);

(Replace the relation REL between the nodes %B1 and %B2 and the relation REL between the nodes %B1 and %B3 by a linear relation between %B1 and %B2)

FINAL STATE: L(%A;%B) L(%B;%C) L:B(%B1;%B2)

The node %B3 is deleted, because it does not have any other relation with any other node inside the hyper-node.

TL#2: REL(%B1;%B2):=(%B2);

(Replace the relation REL between the nodes %B1 and %B2 by the node %B1)

FINAL STATE: L(%A;%B) L(%B;%C) REL:B(%B1;%B3) :B(%B2)

The node %B1 is not deleted, because it still has a relation with the node %B3. The relation between %B1 and %B2 is replaced by a single node %B2.

TT or NN Rules

INITIAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) REL:B(%B1;%B4)

TT#1:REL(%x;%y):=NEWREL(%x;%y)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) NEWREL:B(%B1;%B4)

The relation is changed, but the arguments %x and %y are preserved.

TT#2: REL(%x;%y):=REL(%w;%z)

FINAL STATE: L(%A;%B) L(%B;%C) L(%C;%D) L:B(%B1;%B2) L:B(%B2;%B3) :B(%B4) REL(%w;%z)

The relation between %x and %y is deleted, but the nodes are preserved. Noticed that %B4 became an isolated node, but it’s still there, because no node may be deleted by a NN rule.

INITIAL STATE : REL(%x;%y;%z)

TT#3:REL(%x;%y;%z):=REL(%x;%y);

FINAL STATE: REL(%x;%y) (%z)

The node %z is not deleted.